El teorema relaciona un lado de un triángulo cualquiera con los otros dos y con el coseno del ángulo formado por estos dos lados:
Teorema del coseno |
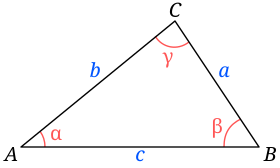
El teorema y sus aplicaciones
El teorema del coseno es también conocido por el nombre de teorema de Pitágoras generalizado, ya que el teorema de Pitágoras es un caso particular: cuando el ángulo es recto o, dicho de otro modo, cuando
es recto o, dicho de otro modo, cuando 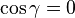 , el teorema del coseno se reduce a:
, el teorema del coseno se reduce a:que es precisamente la formulación del teorema de Pitágoras.
El teorema se utiliza en triangulación (ver Fig. 3) para resolver un triángulo, y saber determinar
- el tercer lado de un triángulo cuando conocemos un ángulo y los lados adyacentes:
.
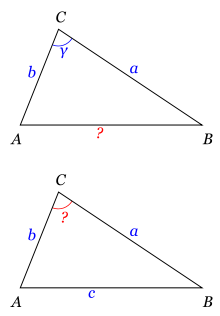
- los ángulos de un triángulo cuando conocemos los tres lados:
Estas fórmulas son difíciles de aplicar en el caso de mediciones de triángulos muy agudos utilizando métodos simples, es decir, cuando el lado c es muy pequeño respecto los lados a y b —o su equivalente, cuando el ángulo γ es muy pequeño..
Existe un corolario del teorema del coseno para el caso de dos triángulos semejantes ABC y A'B'C'
.
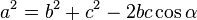









0 comentarios:
Publicar un comentario